Learn Mathematical Modeling
Mathematical modeling is the art and skill of translating real problems into mathematics. It captures the essence, the pattern and the structure of a problem and formulates them in a formal way.
For whom: Modeling language designers, Students in business analytics, operation research, operations management, and all persons interested in mathematical applications.
Start learning Help
Step 01: Learn What modeling is
Learn the defintions of "model". Get familiar with other modeling concepts. Find out what a mathematical model is.

model ≡ representation of knowledge
A model is a description or a representation of an object, a system or a process in order to understand
or explain how it works. It structures knowledge in order to make decisions, it helps to control the
environment, and to predict events.
Bohr's atom model, consisting of a dense nucleus surrounded by orbiting electrons is an
approximation of the "atom". The orbits are labeled by an integer, the quantum number. Electrons can jump
from one orbit to another by emitting or absorbing energy. It explains how electrons can have stable orbits
around the nucleus and why atoms had characteristic emission spectra. It is still used to introduce students
to quantum mechanics.

modeling ≡ problem solving ≡ science
Modeling means capturing the essence, the pattern and the structure of a problem and to formulate it in a
precise way. It makes abstraction of the unessential.
Planning to install semaphores on a street junction is a problem that can be translated
into vertex coloring of a graph: The street lanes are mapped to the vertices and
conflicting lanes to edges. Vehicules on lanes with the same color can traverse the junction at the same
time without
collision. The goal is to have the least number of colors (semaphore phases).
People with modeling skills are in high demand, because formal models are pervading the industrial and economical processes: planning workforce, production planning, route planning, sport scheduling.

Math modeling ≡ Insight, not numbers
The power of abstraction, this ability to leave out some or many details about a concrete problem in order
to use the "distillate" for a multitude of similar problems, is one of the most striking characteristics of
our mind. Mathematics and logic are essential tools in the process of abstraction.
A mathematical model consists of symbols like operations, numerical data, variables (the
unknowns), and constraints. It is the results of a abstraction process and is a powerful language
to express, represent, analyse, and provide insight into real-world phenomena. Once a real problem is
formulated as a mathematical model, it
can be solved using powerful computer tools.
Step 02: Learn how to build models
Building models is a skill that must be learnt. A lot of experience is needed to create good models. The huge material proposed here gives useful guidelines by means of many case studies. Five simple examples are presented below.
01 very easy
How old is Peter ?
Peter's age is a third of his father's age, but in 10 years his father will only be two times as old as
Peter will be.
What is Peter's age today?
(This is the kind of problems the reader probably has seen in primary school in mathematics. Is it easy?
Then go to the next, otherwise follow carefully the explanation in the "solution" link below!)

02 easy
3-jugs problem
There are 3 jugs with capacities of 8, 5, and 3 liters. Initially, the 8-liter jug is full of water,
whereas the others are empty. Find a sequence for pouring the water from one jug to another such that
the end result
is to have 4 liters in the 8-liter jug and the other 4 liters in the 5-liter jug. When pouring the water
from a jug A into another jug B, either jug A must be emptied or B must be filled.
(This problem is a gentle introduction of graphs, an important concept in modeling in general.)

03 easy, but...
Seven digits puzzle
Use each digit from 1 to 7 exactly once, and place them into the circles A to G of the Figure in such a
way that
the sum along each of the five straight lines is the same.
(One may solve this problem without mathematics just by trying. The mathematics here is a little bit more
involving. The concept of indexes is used. Not familiar with them? Then go to Help. More help is given there.)

04 not so easy
The clock problem
Divide the clock with a straight cut into two parts such that the sum of the numbers in both parts are
equal?
(This problem seems particularly easy. It is not! Well by trying the reader get quickly a solution. But
then the question arises: It this te unique solution? How can one find all? The resulting mathematical
model uses binary variables and logical conditions. Doesn't sound familiar? Then go to Help. More help is given there.)

05 difficult
Six snakes problem
The 6-snakes problem is a board game for one person. The board is a hexagon with 72 notches where the 72 pellets must be placed. The pellets are divided into 6 groups of 12 pellets with the same color. In each group, exactly one pellet is a little bit larger that is called the "head of the snake". The inital situation of the game is to place the 6 heads of the snakes anywhere in a notch of the board. The goal is to place all other pellets such that the pellets with the same color form a "snake" on the board starting with the head of the snake, that is, each following pellets with the same color must be neighbor of the previous pellet with the same color and the snake cannot cross over another snake.

HINT:
Let x be the age of Peter today, and y be the age of his father today. Can you write down the conditions now?"
SOLUTION:
The age of the father is y, and also 3x (he is three times as
old as his son), hence: y = 3x. In ten year, the father is y+10 year old,
but
also 2(x+10), hence: y+10 = 2(x+10).
Therefore, the mathematical model
is:
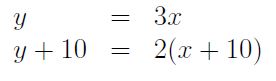
HINT:
A state is a possible filling of the three jugs and can be represented as a triple of numbers. For example: The triple (8,0,0) means "the 8L-jug is full, the others are empty". Enumerate all states and list all transitions from one to another state.
SOLUTION:
The resulting model is a directed graph with 16 states, in which a shortest path is to be found. The "shortest path" problem is a well known problem in operations research.
HINT:
Think about what digit to put in the middle circle D to solve it by thinking. However, we want to solve the problem with a mathematical model. Introduce 7 integer variables: in each circle with a different value from 1 to 7.
SOLUTION:
All variables must have a different value from 1 to 7 and the sum of the three corresponding variables on a line must all be the same. For a complete model click below.
HINT:
Draw a line from the smallest to the largest number (1 and 12), then draw a line from the the second largest to the second smallest number (2 and 11). Do you see the pattern?
SOLUTION:
Continuing this way (drawing the parallel lines), there sum is always 13. Three lines are above and three lines are below the cut. That's it! However, now formulate this in a mathematical model. For each number from 1 to 12, introduce a binary variable. The variable is 1, if the number is on one side of the cut and 0 otherwise. Then the model has two constraints: (1) The sum of the numbers on one side must by half of the sum of all numbers. (2) Exactly two consecutive variables have different values. For a complete model click below.
HINT:
A snake consists of 12 pellets each with a position within the snake (the head of the snake is position 1, the next is position 2, and so on). Each pellet (72) is to be placed in a particular notch on the board. Basically, we need to know which notch belongs to which snake at which position within the snake.
SOLUTION:
It is a bit involving to explain the solution here. If you are interested, open the link below.
Step 03: Learn how to implement models
Quickly a model becomes too complicated to be solved manually. The problem then is
to
find the right tools to formulate the problem on a computer. Basically, what we need is:
→ a software that represents the problem and
→ a software that solves the model.
The main tool used here to represent a model is the modeling language called LPL. The basics are easy to learn and initially there is no need to install any software. The models can directly be solved through the Internet. (Other tools are presented later.)
How old is Peter (Solution)
The complete mathematical model is as follows:
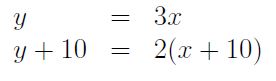
It is easy to solve these two equations by hand: (1) Substitute y in the second equation by 3x, and then (2) solve it for x.
LPL code for the problem
model AgeOfPeter "How old is Peter";
variable x; y;
constraint A: y = 3*x;
B: y+10 = 2*(x+10);
solve;
Write('The age of Peter is: %d\n', x);
end
Copy this code and paste it HERE.
Then click
the
button
"RUN and SOLVE".
Seven digits puzzle (Solution) ?
The complete mathematical model is as follows:
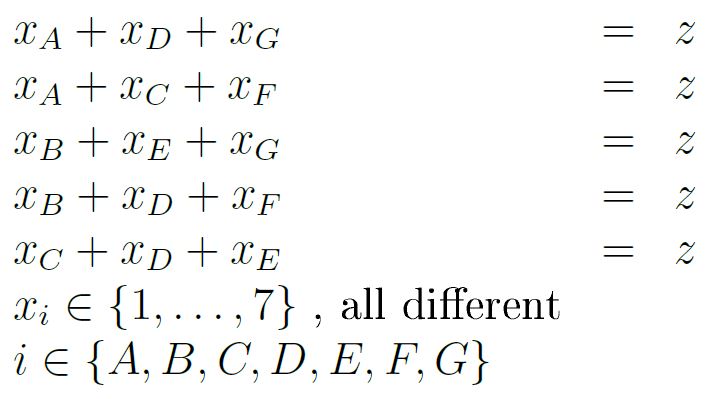
It is a little bit more complicated to solve this probem.
LPL code for the problem
model Puzzle7 "The 7-Digits Puzzle";
set i,j := ['A','B','C','D','E','F','G'];
alldiff variable x{i} [1..7]; variable z;
constraint
L1: x['A'] + x['D'] + x['G'] = z;
L2: x['A'] + x['C'] + x['F'] = z;
L3: x['B'] + x['E'] + x['G'] = z;
L4: x['B'] + x['D'] + x['F'] = z;
L5: x['C'] + x['D'] + x['E'] = z;
solve;
Write('%s , z=%d\n',
{i} Format('%s=%d ', i, x), z));
end
Copy this code and paste it HERE.
Then click
the
button
"RUN and SOLVE".
The clock problem (Solution) ?
The complete mathematical model is as follows:
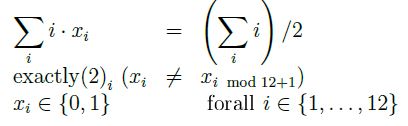
There is already some modeling knowledge needed to understand this formulation.
LPL code for the problem
model DivideClock;
set i := 1..12;
binary variable x{i};
constraint A: sum{i} i*x = (sum{i} i)/2;
B: exactly(2){i} (x[i]<>x[i%#i+1]);
solve;
Write('Numbers: %3d on one side\n',
{i|x} i);
end
Copy this code and paste it HERE.
Then click
the
button
"RUN and SOLVE".
